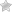- Компания Xi3 Corporation представила два модульных компьютера серии Xi3 Modular – X7A и X3A.
- Кроме того, компания объявила о снижении стартовой цены с $899 до $499 на отмеченный наградами модульный компьютер X5A-5342.

Проект, представленный Xi3 на сайте Kickstarter («Xi3: Help us Usher in the Post-PC Era» или «Xi3: помогите нам вступить в пост-ПК эру»), позволяет заинтересованным лицам узнать о планах Xi3 относительно двух новых модульных компьютеров, а также сделать предзаказ на X7A и X3A. Более того, инвесторы, внесшие залог при предзаказе модели X7A или X3A, получат свой модульный компьютер за де недели до начала общих продаж и приобретут право и в дальнейшем получать заранее заказанную продукцию компании Xi3 до сроков ее официального выхода на рынок.
Модульный компьютер X7A (для опытных пользователей, геймеров и инженеров)
Новый модульный компьютер X7A разработан специально для геймеров, инженеров и опытных пользователей. Помещенная в стандартный корпус компании Xi3, имеющий размеры 10.85 × 9.29 × 9.29 см, модель X7A демонстрирует реальную мощь, являясь при этом вычислительной машиной величиной с грейпфрут и потребляющей всего 40 Вт.

Модульный компьютер X7A поставляется в следующей комплектации:
- Четырехъядерный 64-разрядный процессор на базе архитектуры x86, выполненный по 32 нм технологии и работающий на тактовой частоте до 3.2 ГГц (с 4 МБ кэша второго уровня)
- Встроенный графический процессор, содержащий до 384 программируемых графических ядер (или шейдеров)
- ОЗУ от 4 до 8 ГБ DDR3
- Емкость встроенного твердотельного накопителя от 64 ГБ до 1 ТБ (с пропускной способностью до 12 Гбит в секунду)
- Три порта для подключения дисплеев с максимальным разрешением 4096 × 2160 (один DisplayPort v1.2 и два Mini-DisplayPorts v1.2)
- Четыре порта eSATAp 3.0
- Четыре порта USB 3.0
- Четыре порта USB 2.0
- Порт гигабитного Ethernet
- Три аудио порта (один вход и 2 выхода: один для подключения медных кабелей, другой – оптоволоконных)
Способный работать как автономно, так и совместно с другими компьютерами в кластерной структуре, X7A поддерживает любую совместимую с x86 операционную систему, включая Windows 8 и предыдущие версии этой ОС, а также Linux, UNIX и т.д. Стартовая цена четырехядерной версии X7A составит $1,100, а начало официальных продаж запланировано на февраль 2013 года.
Модульный компьютер X3A (бюджетная модель компьютера)

В отличие от X7A, модульный компьютер X3A предназначен для использования в качестве стандартного домашнего или офисного компьютера. X3A доступен в следующей конфигурации:
- Двухъядерный 64-разрядный процессор на базе архитектуры x86, работающий на тактовой частоте до 1.65 ГГц (с 2 МБ кэша второго уровня)
- Встроенный графический процессор, содержащий до 80 программируемых графических ядер (или шейдеров)
- ОЗУ 4 ГБ DDR3
- Емкость встроенного твердотельного накопителя от 32 ГБ до 1 ТБ (с пропускной способностью до 12 Гбит в секунду)
- Два порта для подключения дисплеев с максимальным разрешением 2560 × 1600 (один HDMI/DisplayPort v1.2 и один Mini-DisplayPort v1.2)
- Четыре порта eSATAp 3.0
- Два порта USB 3.0
- Четыре порта USB 2.0
- Порт гигабитного Ethernet
- Три аудио порта (один вход и 2 выхода: один для подключения медных кабелей, другой – оптоволоконных)
Модульный компьютер X3A потребляет 18 Вт и поддерживает любую совместимую с x86 операционную систему, включая Windows 8 и предыдущие версии этой ОС, а также Linux, UNIX и т.д. Стартовая цена двухъядерной версии X3A составляет $499, а выход продукта на рынок запланирован на январь 2013 года.
Начальная цена за модель X5A-5342 снижена до $499
Самый первый модульный компьютер компании Xi3 (модель X5A-5342) был представлен в январе 2011 года на международной выставке CES, проходившей в Лас-Вегасе, штат Невада.
Позже в том же году начались поставки X5A-5342, и в настоящее время этот компьютер используется по всему миру различными национальными и местными правительственными учреждениями и департаментами, учебными заведениями, крупными корпорациями, малым бизнесом и обычными пользователями.
Учитывая затянувшийся релиз новых модульных компьютеров X7A и X3A, а также предстоящий выпуск microSERV3R, Xi3 решила значительно снизить стартовую цену на X5A-5342 сразу с $899 до $499.
Модель X5A-5342 поддерживает любую совместимую с x86 операционную систему и потребляет 20 Вт. Ее технические характеристики следующие:
- Двухъядерный 64-разрядный процессор на базе архитектуры x86, работающий на тактовой частоте до 1.8 ГГц (с 1 МБ кэша второго уровня)
- Встроенный графический процессор
- ОЗУ 2 ГБ DDR3
- Емкость встроенного твердотельного накопителя от 16 ГБ до 1 ТБ
- Два порта для подключения дисплеев с максимальным разрешением 2560 × 1600 (один с поддержкой DVI-DL + VGA / DVI-DL + DP / VGA + DP и один с DP/DVI)
- Два порта eSATAp 2.5
- Шесть портов USB 2.0
- Порт гигабитного Ethernet
- Три аудио порта
Значительные преимущества модульных компьютеров Xi3
Каждый модульный компьютер компании Xi3
- Представляет собой компьютер в компактном корпусе размером с небольшой мяч (10.85 × 9.29 × 9.29 см)
- Потребляет намного меньше энергии (во многих случаях в десять раз меньше), чем другие компьютеры со схожими характеристиками (40 Вт для X7A, 20 Вт для X5A-5342 и 18 Вт для X3A)
- Использует запатентованную трехплатную конструкцию компании Xi3
- Может быть обновлен, модернизирован, изменен и/или отремонтирован путем замены одной из трех плат на новую

Xi3, Valve объединяет усилия на компактном игровом ПК для вашего HDTV 2022
LAS VEGAS— Модульный производитель ПК Xi3 делает несколько довольно маленьких машин, и теперь мы знаем, что он работает над чем-то большим.
Компания работает на мини-ПК, который достаточно мал, чтобы вписаться в вашу руку, но достаточно мощный, чтобы играть в компьютерные игры среднего уровня на HD-дисплее.
Более того, Valve Software инвестирует в компанию, чтобы помочь им снять ее.

Прототип называется Piston: Xi3 утверждает, что машина оптимизирована специально для игр на ПК на дисплеях HD и обещает поддержку онлайн-игровой платформы Valve Steam.
Ни одна из компаний не скажет, будет ли компактная машина представлять собой раннюю версию игрового ПК с паролями «Steam Box» с длинными слухами, который будет использовать режим Big Picture в режиме «Фото», чтобы подключиться к HDTV и функционировать как традиционные игровые консоли.
Вот что мы Известно, что прототип Xi3's Piston основан на его новом модульном компьютере X7A, который имеет начальную розничную цену примерно в 1000 долларов.
Xi3 не будет раскрывать информацию о том, что находится внутри поршня, или сколько это будет стоить, но мы знаем, что X7A сумеет втиснуть четырехъядерный AMD APU, до 8 ГБ оперативной памяти DDR3 и SSD объемом 32 ГБ в корпусе размером чуть более 4 дюймов длинный и 3 дюйма в высоту.
Xi3 вытаскивает его, разбивая стандартную материнскую плату ПК на три небольших секции и разбивая эти фрагменты внутри X7A. Модернизация материнской платы будет сложной и потенциально невозможной процедурой, но должно быть довольно легко взломать корпус, чтобы поменять остальные компоненты.

Прототип Xi3 Piston предлагает множество портов
Но X7A isn разработанный с учетом энтузиастов ПК; он предназначен для использования в качестве рабочей станции или домашнего ПК для развлечений, а прототип Piston имеет аналогичную привлекательность.
Это небольшая, гладкая матовая черная машина, которая прекрасно вписывается в ладонь вашей руки, и есть даже настраиваемая монтажная скоба, которую вы можете использовать для установки одного из этих модульных компьютеров в ваш HDTV или домашний развлекательный центр.
Задняя панель устройство оснащено портами, в том числе 12 портами USB (как 2.0, так и 3.0), аудиовходом / выходом, гнездом Gigabit Ethernet, 2 мини-разъемами DisplayPort и комбинированным разъемом HDMI / DisplayPort.
Учитывая, насколько крошечными эти модульные компьютеры, шведский стол портов предполагает, что вы можете уйти с собой и использовать его для работы, развлечений или игры с равным апломбом.
Нет ни слова о том, какую производительность мы можем ожидать от этого прототипа, но нетрудно представить себе ближайшее будущее, в котором Piston PC поставляется с кабелем HDMI и игровым контроллером для продажи в торговых точках в качестве выделенного игрового ПК для в гостиной.
Чтобы узнать больше блогов, рассказов, фотографий и видео из крупнейшей в стране выставки бытовой электроники, просмотрите полный охват CES 2013 от PCWorld и TechHive.
Модульный ПК — Xi3 Modular Computer
Американская компания Xi3 официально представила модульный компьютер Xi3 Modular Computer, который воплотил в себе инновационные представления компании о современном компьютере.
Этот компактный ПК выполнен в форме куба с размерами сторон 101.6 х 92,8 х 92,8 мм. Корпус новинки отличается необычной конструкцией выполнен из алюминия и выполняет функции радиатора для отвода тепла.
Материнская плата делится на три отдельные части – на одной содержится процессор и оперативная память, на остальных интерфейсы ввода/вывода и другие компоненты.
Каждый из модулей Xi3 может быть удален, изменен и/или заменен.
Все версии этого компьютера оснащены процессором AMD Athlon 64. В продаже сначала будут доступны три модели Xi3: с процессором Athlon 64 2000 с тактовой частотой 1 ГГц, Athlon 64 3400e с частотой 1,8 ГГц и 2,2 ГГц процессором Athlon 64 4200 +.
Также Xi3 Modular Computer оснащен интегрированной графикой DX10, которая обеспечивает воспроизведение видео высокой четкости в форматах вплоть до 1080p, имеет до 4 Гб оперативной памяти, сетевой контроллер Gigabit Ethernet, аудио и видео выходы, шесть портов USB 2.0, два разъема ESATA, DVI, DisplayPort и HDMI выход.
Энергопотребление компьютера с процессором Athlon 64 2000+ составляет около 20 Вт.
“Мы отвергаем представления о том, что компьютеры должны иметь срок полезного использования только от двух до четырех лет”,- говорит Джейсон А. Салливан (Jason A. Sullivan), президент и главный исполнительный директор корпорации Xi3.
“Вместо того мы считаем, что компьютеры должны быть обновляемым снова и снова и снова, и для этого мы разработали Xi3 Modular Computer, что делает его (потенциально) последним компьютером, который вам когда-либо надо будет приобрести.
”
Модульный компьютер Xi3 уже заслужил награду Международной выставки CES 2011, открывающейся в Лос-Анджелесе в январе, за инновации в категории Компьютеры и комплектующие .
Младшая модель системы с 1 ГГц процессором Athlon 64 2000 поступила в ограниченную продажу в США по цене 849 долларов. В широкую продажу устройство поступит в начале 2011 года.
Калькулятор комлексных чисел | Вычисление выражений, содержащих комплексные числа
- Главная
- /
- Калькуляторы
- /
- Калькулятор комплексных чисел
Калькулятор комплексных чисел позволяет вычислять арифметические выражения, содержащие комплексные числа, знаки арифметических действий (+, -, *, /, ^), а также некоторые математические функции.
Калькулятор комплексных чисел
- 7
- 8
- 9
- +
- —
- *
- /
- ^
- 4
- 5
- 6
- i
- (
- )
- π
- e
- 1
- 2
- 3
- sin
- cos
- tg
- ctg
- ln
- .
- √
- sh
- ch
- th
- cth
- abs
Скрыть клавиатуру
Вычислено выражений:
Как пользоваться калькулятором
- Введите в поле ввода выражение с комплексными числами
- Укажите, требуется ли вывод решения переключателем «С решением»
- Нажмите на кнопку «Построить»
комплексные числа можно вводить в следующих трёх форматах:
- Только действительная часть: 2, 2.5, -6.7, 12.25
- Только мнимая часть: i, -i, 2i, -5i, 2.16i, -12.5i
- Действительная и мнимая части: 2+i, -5+15i, -7+2.5i, -6+i
- Математические константы: π, e
Поддерживаемые операции и математические функции
- Арифметические операции: +, -, *, /, ^
- Получение абсолютного значения числа: abs
- Базовые математические функции: exp, ln, sqrt
- Получение действительной и мнимой частей: re, im
- Тригонометрические функции: sin, cos, tg, ctg
- Гиперболические функции: sh, ch, th, cth
- Обратные тригонометрические функции: arcsin, arccos, arctg, arcctg
- Обратные гиперболические функции: arsh, arch, arth, arcth
Примеры корректных выражений
- (2+3i)*(5-7i)
- sh(i)
- (4+i) / (3 — 4i)
- sqrt(2i)
- (-3+4i)*2i / exp(2i + (15 — 8i)/4 — 3.75)
Комплексные числа — это числа вида x+iy, где x, y — вещественные числа, а i — мнимая единица (специальное число, квадрат которого равен -1, то есть i2 = -1).
Так же, как и для вещественных чисел, для комплексных чисел определены операции сложения, разности, умножения и деления, однако комплексные числа нельзя сравнивать.
Примеры комплексных чисел
- 4+3i — действительная часть = 4, мнимая = 3
- -2+i — действительная часть = -2, мнимая = 1
- i — действительная часть = 0, мнимая = 1
- -i — действительная часть = 0, мнимая = -1
- 10 — действительная часть = 10, мнимая = 0
Основные действия с комплексными числами
Основными операциями, определёнными для комплексных чисел, являются сложение, разность, произведение и деление комплексных чисел. Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:
- сложение: (a + bi) + (c + di) = (a + c) + (b + d)i
- вычитание: (a + bi) — (c + di) = (a — c) + (b — d)i
- умножение: (a + bi) · (c + di) = ac + bci + adi + bdi2 = (ac — bd) + (bc + ad)i
- деление: = = + i
Примеры
Найти сумму чисел 5+7i и 5.5-2i:
Найдём отдельно суммы действительных частей и сумму мнимых частей: re = 5 + 5.5 = 10.5, im = 7 — 2 = 5.
Запишем их рядом, добавив к мнимой части i: 10.5 + 5i
Полученное число и будет ответом:5+7i + 5.5-2i = 10.5 + 5i
- Найти разность чисел 12-i и -2i:
Найдём отдельно разности действительных частей и разности мнимых частей: re = 12 — 0 = 12, im = -1 — (-2) = 1.
Запишем их рядом, добавив к мнимой части i: 12 + 1i - Полученное число и будет ответом:12-i — (-2i) = 12 + i
- Найти произведение чисел 2+3i и 5-7i:
Найдём по формуле действительную и мнимую части: re = 2·5 — 3·(-7) = 31, im = 3·5 + 2·(-7) = 1.
Запишем их рядом, добавив к мнимой части i: 31 + 1i - Полученное число и будет ответом:2+3i * (5-7i) = 31 + i
- Найти отношение чисел 75-50i и 3+4i:
Найдём по формуле действительную и мнимую части: re = (75·3 — 50·4) / 25 = 1, im = (-50·3 — 75·4) / 25 = -18.
Запишем их рядом, добавив к мнимой части i: 1 — 18i - Полученное число и будет ответом:75-50i / (3+4i) = 1 — 18i
Другие действия над комплексными числами
Помимо базовых операций сложения, вычитания, умножения и деления комплексных чисел существуют также различные математические функции. Рассмотрим некоторые из них:
- Получение действительной части числа: Re(z) = a
- Получение мнимой части числа: Im(z) = b
- Модуль числа: |z| = √(a2 + b2)
- Аргумент числа: arg z = arctg(b / a)
- Экспонента: ez = ea·cos(b) + i·ea·sin(b)
- Логарифм: Ln(z) = ln |z| + i·arg(z)
- Тригонометрические функции: sin z, cos z, tg z, ctg z
- Гиперболические функции: sh z, ch z, th z, cth z
- Обратные тригонометрические функции: arcsin z, arccos z, arctg z, arcctg z
- Обратные гиперболические функции: arsh z, arch z, arth z, arcth z
Примеры
- Найти действительную и мнимую части числа z, а также его модуль, если z = 4 — 3i
Re(z) = Re(4 — 3i) = 4
Im(z) = Im(4 — 3i) = -3 - |z| = √(42 + (-3)2) = √25 = 5
Формы представления комплексных чисел
Комплексные числа принято представлять в одной из трёх следующих форм: алгебраической, тригонометрической и показательной.
- Алгебраическая форма — наиболее часто используемая форма комплексного числа, запись числа в виде суммы действительной и мнимой частей: x+iy, где x — действительная часть, а y — мнимая часть
- Тригонометричкая форма — запись вида r·(cos φ + isin φ), где r — модуль комплексного числа (r = |z|), а φ — аргумент этого числа (φ = arg(z))
- Показательная форма — запись вида r·eiφ, где r — модуль комплексного числа (r = |z|), e — число Эйлера, а φ — аргумент комплексного числа (φ = arg(z))
Пример:
Переведите число 1+i в тригонометрическую и показательную формы:
Решение:
- Найдём радиус (модуль) комплексного числа r: r = √(12 + 12) = √2
- Найдём аргумент числа: φ = arctan() = = 45°
- Запишем результат в тригонометрической форме: √2·(cos(45°) + isin(45°))
- Запишем результат в показательной форме: √2·eπi/4
Обратный по модулю в кольце
Синонимом к данному выражению является выражение «остаток от деления«. То есть выражение «5 по модулю 3» эквивалентно выражению «остаток от деления 5 на 3». И в том и в другом случае подразумевается в ответе число 2, так как остаток от деления 5 на 3 = 2.
Стоить отметить тот факт, что по модулю m мы имеем числа от 0 до m — 1. Действительно, остаток от деления на m никогда не превысит m — 1.
Что такое обратное?
Напомним, что число, умноженное на его обратное, равно 1. Из базовой арифметики мы знаем, что:
Число, обратное к числу A, равно 1 / A, поскольку A * (1 / A) = 1 (например, значение, обратное к 5, равно 1/5). Все действительные числа, кроме 0, имеют обратную Умножение числа на обратное к A эквивалентно делению на A (например, 10/5 соответствует 10 * 1/5)
Что такое обратное по модулю?
В модульной арифметике у нас нет операции деления. Тем не менее, у нас есть модульные инверсии.
Модульная инверсия a (mod m) есть a-1 (a * a-1) ≡ 1 (mod m) или эквивалентно (a * a-1) mod m = 1 Только числа, взаимно простые с модулем m, имеют модульное обратное.
Говоря проще, обратным элементом к a по модулю m является такое число b, что остаток от деления (a * b) на модуль m равно единице (a * a-1) mod m = 1
Как найти модульный обратный
Наивный метод нахождения модульного обратного a ( по модулю m) является:Шаг 1. Рассчитать a * b mod m для значений b от 0 до m — 1Шаг 2. Модульная инверсия a mod m — это значение b, при котором a * b mod m = 1
Обратите внимание, что термин b mod m может иметь только целочисленное значение от 0 до m — 1, поэтому тестирование больших значений чем (m-1) для b является излишним.
Вы наверно уже догадались, что наивный метод является очень медленным. Перебор всех чисел от 0 до m-1 для большого модуля довольно-таки трудоемкая задача. Существует гораздо более быстрый метод нахождения инверсии a (mod m). Таковым является расширенный алгоритм Евклида, который реализован в данном калькуляторе.
Расширенный алгоритм Евклида
Представим наибольший общий делитель числа a и модуля m в виде ax + my. То есть НОД(a, m) = ax + my. Помним, что обратный элемент существует только тогда, когда a и m взаимно просты, то есть их НОД(a, m) = 1. Отсюда: ax + my = 1 — линейное диофантово уравнение второго порядка. Необходимо решить данное уравнение в целых числах и найти x, y.
Найденный коэффициент x будет являться обратным элементом к a по модулю m. Это следует оттуда, что, если мы возьмём от обеих частей уравнения остаток по модулю m, то получим: ax = 1 (m).
Расширенный алгоритм Евклида, в отличие от классического, помимо наибольшего общего делителя позволяет найти также коэффициенты x, y.
Алгоритм:
Вход: a, m ≠ 0
Выход: d, x, y, такие что d = gcd(a, m) = ax + my
1. [Инициализация] (a0, a1) := (a, m); (x0, x1) := (1, 0); (y0; y1) := (0, 1).
- 2. [Основной цикл] Пока a1 ≠ 0 выполнять {q = QUO(a0, a1);(a0, a1) := (a1, a0 — a1q); (x0, x1) := (x1, x0 — x1q); (y0, y1) := (y1, y0 — y1q);
- QUO(a0, a1) — целая часть от деления a0 на a1
- 3. [Выход] Вернуть (d, x, y) = (a0, x0, y0)
- Битовая сложность расширенного алгоритма Евклида равна O((log2(n))2) , где n = max (|a|, |m|)
Непонятен алгоритм? Ничего страшного, примеры ниже именно для этого и предназначены.
Разбор демоверсии ЕГЭ по информатике 2022 (22-27 Задание)
Продолжаем анализ демонстрационного варианта ЕГЭ по информатике 2022.
В этой статье разберём с 22-ого по 27 задание.
Источник задач: https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-5.
ЕГЭ по информатике 2022 будет повержено!
Разбор демоверсии ЕГЭ по информатике 2022 (1-5 Задание)
Разбор демоверсии ЕГЭ по информатике 2022 (6-10 Задание) Разбор демоверсии ЕГЭ по информатике 2022 (11-15 Задание) Разбор демоверсии ЕГЭ по информатике 2022 (16-21 Задание)
Задание 22
Ниже на четырёх языках программирования записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: L и M. Укажите наибольшее число x, при вводе которого алгоритм печатает сначала 4, а потом 5.
- Решение:
- Решение данного задания будет похоже на решение 6 задания из ЕГЭ по информатике 2022.
- С помощью перебора на языке Python найдём при каких значениях переменная L=4 И переменная M=5 в конце программы.
for i in range(1, 1000): X=i Q=9 L=0 while X >= Q: L = L + 1 X = X — Q M=X if M < L: M = L L = X if L==4 and M==5: print(i)
Наибольшее значение равно 49.
Ответ: 49 Смотреть 22 Задание на YouTube
- Задание 23
- Исполнитель преобразует число на экране.
- У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1 2. Умножить на 2
Программа для исполнителя – это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 20, и при этом траектория вычислений содержит число 10?
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17.
Решение:
Решим задачу c помощью шаблона на языке Python.
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x*2, y) print(F(1, 10)*F(10, 20))
Число x, это то число, с которым мы работаем. Число y — это куда нужно прийти.
Если число x достигло пункта назначения, то возвращаем 1. Если оно перескочило y, то возвращаем 0. А если ещё не дошло до y, то продолжаем вычисления с помощью рекурсии.
У нас число 10 обязательное, поэтому разбиваем функцию следующим образом F(1, 10)*F(10, 20), через умножение. Это и будет ответ. Получается 28.
Ответ: 28 Смотреть 23 Задание на YouTube
- Задание 24
- Текстовый файл состоит из символов P, Q, R и S.
Определите максимальное количество идущих подряд символов в прилагаемом файле, среди которых нет идущих подряд символов P. Для выполнения этого задания следует написать программу.
Решение:
Напишем решение на языке Python.
f=open('24.txt') s=f.read() count=1 mx=0 for i in range(0, len(s)-1): if s[i]=='P' and s[i+1]=='P': count=1 else: count=count+1 mx = max(mx, count) print(mx)
Подсчитываем символы, пока не встретилась комбинация двух P подряд. Как только встретилась данная комбинация, сбрасываем счётчик на 1. Здесь мы сбрасываем счётчик на значение 1, чтобы учесть один символ, которые находится в самой комбинации PP. И в начале мы тоже устанавливаем счётчик в значение 1 по этой же причине.
Мы проходим в цикле for до длины строки минус один. Значение 1 в счётчике при сбросе и в начале программы так же компенсирует и тот момент, что мы не подсчитываем последний символ!
- При изменении счётчика, сохраняем максимальное значение в переменной mx
- Если бы у нас была вместо PP другая комбинация, состоящая к примеру из 5 символов, то мы бы тогда в начале и при сбросе писали в счётчик значение 5-1=4.
- В этой задаче получается ответ 188.
Ответ: 188 Смотреть 24 Задание на YouTube
Задание 25
Пусть M – сумма минимального и максимального натуральных делителей целого числа, не считая единицы и самого числа. Если таких делителей у числа нет, то значение M считается равным нулю.
Напишите программу, которая перебирает целые числа, бо́льшие 700 000, в порядке возрастания и ищет среди них такие, для которых значение M оканчивается на 8. Выведите первые пять найденных чисел и соответствующие им значения M.
Формат вывода: для каждого из пяти таких найденных чисел в отдельной строке сначала выводится само число, затем – значение М. Строки выводятся в порядке возрастания найденных чисел.
Количество строк в таблице для ответа избыточно.
Решение:
На ЕГЭ по информатике 2022 удобно писать программы на языке Python.
import math count=0 for i in range(700001, 800000): b=0 for j in range(2, int(math.sqrt(i)) + 1): if i%j==0: b=round(i/j) break if b==0: M=0 else: M=j+b if M!=0 and M%10==8: count=count+1 print(i, M) if count==5: break
В данной программе перебираются числа в цикле for, начиная с 700001.
Переменная b-считается наибольшим делителем числа i. Затем, с помощью ещё одного цикла for перебираются числа с 2 до корня числа i (включительно). Ищем тем самым наименьший делитель.
Если до корня числа включительно не встретился ни один делитель, значит, у числа нет делителей, кроме 1 и самого числа.
Пусть у нас есть число A. Если у этого числа есть делитель d1, то он находится до корня этого числа. А вот то число (так же делитель), на которое умножается это число d1, чтобы получить A, будет находиться после корня A.
Получается, что у каждого делителя есть своя пара. У единицы — это само число. Причём один делитель из пары находится до корня, другой после корня. Исключением будет тот случай, когда из числа А извлекается целый корень. Тогда для этого корня не будет пары (парой и будет само это число √A * √A = A).
Таким образом, первый найденный делитель будет являться наименьшим делителем. А вот делительный, который находится в паре с наименьшим делителем, будет наибольшим.
После того, как мы нашли наименьший делитель (он будет сидеть в переменной j) и наибольший делитель b, выходим из второго цикла for.
Если переменная b осталась равна нулю, то, значит, у числа i нет указанных делителей, и переменная M должна равняться 0. Если b не равна нулю, то M=j+b.
Проверить, на что оканчивается число, можно узнав остаток от деления числа на 10.
Переменная count следит, чтобы было распечатано ровно 5 чисел, которые удовлетворяют условию задачи.
Ответ:
| 700005 | 233338 |
| 700007 | 100008 |
| 700012 | 350008 |
| 700015 | 140008 |
| 700031 | 24168 |
Смотреть 25 Задание на YouTube
Задание 26
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов.
- Известно, какой объём занимает файл каждого пользователя.
- По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
- Входные данные.
В первой строке входного файла находятся два числа: S – размер свободного места на диске (натуральное число, не превышающее 10 000) и N – количество пользователей (натуральное число, не превышающее 1000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое – в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем – максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Пример входного файла:
100 4 80 30 50 40
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов – 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар – 50, поэтому ответ для приведённого примера:
2 50
Решение:
Решим задачу с помощью Excel. Чтобы открыть текстовый файл в программе Excel, выбираем Файл->Открыть, выбираем нужную папку и указываем, чтобы в папке были видны все типы файлов.
И выбираем наш текстовый файл.
Выскочит окно Мастер текстов (импорт). Здесь оставляем выбранный пункт с разделителями и кликаем Далее.
В следующем окне поставим ещё галочку пробел. В итоге Символами-разделителем будут знак табуляции и пробел.
Кликаем ещё раз Далее и Готово.
Наши данные вставятся, как нужно!
Число 8200 (размер свободного места) нужно запомнить или записать на черновике. Число 970 (количество файлов) нам в принципе не нужно при таком подходе решения.
Теперь удаляем первую строчку. Выделяем две ячейки в первой строчке, через контекстное меню мыши нажимаем Удалить…. Выбираем ячейки, со сдвигом вверх.
1. Найдём максимальное количество файлов.
Выделяем весь столбец A и сортируем его по возрастанию.
Теперь выделяем ячейки сверху мышкой, а справа в нижней части программы будет показываться сумма выделенных ячеек.
Мы должны выделить максимальное количество ячеек, но чтобы сумма не превышала число 8200.
Получается максимальное количество файлов, которое можно сохранить, равно 568.
2. Найдём максимальный размер файла при максимальном количестве файлов.
Если мы сохраним максимальное количество файлов, то у нас ещё останется свободное место 8200-8176=24, т.к. сумма выделенных ячеек равна 8176.
Мы можем заменить наибольший файл (последняя выделенная ячейка равная 29) ещё большим файлом, размер которого не превышает 24+29=53.
Если покрутим таблицу вниз, то найдём такой файл размером 50. Это и будет наибольший файл при максимальном количестве файлов.
Ответ: Смотреть 26 Задание на YouTube
Задание 27
Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, такие что сумма элементов каждой из них кратна k = 43. Найдите среди них подпоследовательность с максимальной суммой, определите её длину. Если таких подпоследовательностей найдено несколько, в ответе укажите количество элементов самой короткой из них.
Входные данные
Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество чисел N (1 ≤ N ≤ 10 000 000). Каждая из следующих N строк содержит одно натуральное число, не превышающее 10 000.
- Пример организации исходных данных во входном файле:
- В ответе укажите два числа: сначала значение искомой суммы для файла А, затем – для файла B.
- Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
- Решение:
- Напишем программу на Python.
7 1 3 4 93 8 5 95 f=open('27_B.txt') n=int(f.readline()) sum_ost=[1096594666]*43 #Массив, который содержит минимальные суммы для разных остатков k=[0]*43 #Запоминаем, при каком i сохранили в sum_ost очередную сумму. mx=0 #Максимальная сумма нужной цепочки в данный момент времени ln=0 #Длина нужной цепочки s=0 #Сумма цепочки с первого до i-ого элемента sum_ost[0]=0 #Для остатка ноль ничего от s отнимать не нужно k[0]=-1 #Для остатка ноль индекс равен -1, чтобы правильно считалась длина цепочки for i in range(n): x=int(f.readline()) s = s + x ost = s % 43 if s-sum_ost[ost]==mx: ln=min(ln, i — k[ost]) if s-sum_ost[ost] > mx: mx = s — sum_ost[ost] ln = i — k[ost] if sum_ost[ost]==1096594666: sum_ost[ost] = s k[ost] = i print(ln)
Переменная s — это сумма от первого до текущего элемента i. На каждом шаге вычисляется остаток от деления s на 43. И записывается в массив sum_ost эта сумма s для каждого остатка.
Тогда кандидатом для ответа будет цепочка, которая получается, если от цепочки с суммой s «отрезать» цепочку с суммой из массив sum_ost, которая соответствует текущему остатку (переменная ost).
В массив sum_ost для каждого остатка записывается сумма только один раз, т.к. нам нужна именно минимальная сумма для каждого остатка, чтобы кандидат для ответа был как можно больше.
В начале массив sum_ost инициализируется очень большим числом 1096594666. Это число больше, чем сумма всех элементов в файле. Оно было найдено до основного решения, с помощью простой программы.
В процессе решения мы ищем среди кандидатов для ответа цепочку с максимальной суммой. Делаем это стандартным образом: кто больше, то и победил. Мы инициализируем большими числом 1096594666 элементы массива sum_ost для того, чтобы условие нормально сработало, когда в массиве sum_ost ещё нет суммы для данного остатка.
Так же мы сохраняем индексы элементов в массив k, когда записываем суммы для различных остатков в массив sum_ost. Это делается для того, чтобы можно было вычислить длину цепочки.
Для случая, когда остаток равен 0, устанавливаем сумму в массиве sum_ost равной нулю, потому что кандидатом на ответ будет цепочка от самого первого до i-ого элемента. Это, можно сказать, исключительный случай. И чтобы правильно вычислялась длина цепочки, для случая, когда остаток равен нулю, индекс в массив k делаем равным -1.
Ответ: Разбор демоверсии ЕГЭ по информатике 2022 (1-5 Задание) Разбор демоверсии ЕГЭ по информатике 2022 (6-10 Задание) Разбор демоверсии ЕГЭ по информатике 2022 (11-15 Задание) Разбор демоверсии ЕГЭ по информатике 2022 (16-21 Задание) Смотреть 27 Задание на YouTube